生成对抗网络 (Generative Adversarial Networks)

引言

我们现在转向另一种称为生成对抗网络(GANs)的生成模型家族。GANs与我们之前见过的所有其他模型家族（如自回归模型、VAEs和标准化流模型）都不同，因为我们不使用最大似然法来训练它们。

无似然学习 (Likelihood-free learning)

为什么不用最大似然法？实际上，更高的似然值并不一定对应更高的样本质量，这一点并不明确。我们知道最优生成模型将给我们最好的样本质量和最高的测试对数似然。然而，具有高测试对数似然的模型仍然可能产生质量较差的样本，反之亦然。

解释：似然(likelihood)是统计学中的一个概念，表示在给定某模型参数的情况下，观测到特定数据的概率。最大似然法是一种常用的参数估计方法，通过最大化观测数据的似然函数来找到最可能的模型参数。简单来说，它试图找到一组参数，使得模型生成我们观察到的数据的概率最大。

要理解为什么会这样，考虑一些病态情况：我们的模型几乎完全由噪声组成，或者我们的模型简单地记忆了训练集。因此，我们转向无似然训练，希望优化不同的目标函数能够让我们同时获得高似然值和高质量的样本。

回想一下，最大似然要求我们评估数据在我们模型\(p_\theta\)下的似然。设置无似然目标的一种自然方法是考虑双样本检验(two-sample test)，这是一种统计检验，用于确定来自两个分布的有限样本集是否来自同一分布，仅使用来自P和Q的样本。

解释：双样本检验是一种统计方法，用于判断两组样本是否来自同一个分布。它不需要知道分布的具体形式，只需要有来自这两个分布的样本。这与传统的似然方法不同，传统方法需要明确定义概率分布函数。

具体来说，给定\(S_1 = \{\mathbf{x} \sim P\}\)和\(S_2 = \{\mathbf{x} \sim Q\}\)，我们根据\(S_1\)和\(S_2\)的差异计算一个检验统计量\(T\)，当\(T\)小于阈值\(\alpha\)时，接受\(P = Q\)的原假设。

解释：

\(S_1\)和\(S_2\)是从两个不同分布中抽取的样本集

检验统计量\(T\)是一个数值，用来衡量这两组样本的差异程度

阈值\(\alpha\)是我们预先设定的一个标准

原假设是指我们默认认为的情况，这里是假设两个分布相同

如果计算出的统计量小于阈值，我们就认为没有足够的证据拒绝"两个分布相同"这一假设

类似地，在我们的生成建模设置中，我们可以访问训练集\(S_1 = \mathcal{D} = \{\mathbf{x} \sim p_{\textrm{data}} \}\)和\(S_2 = \{\mathbf{x} \sim p_{\theta} \}\)。关键思想是训练模型以最小化\(S_1\)和\(S_2\)之间的双样本检验目标。但这个目标在高维空间中变得极其难以处理，所以我们选择优化一个替代目标，即最大化\(S_1\)和\(S_2\)之间的某种距离。

解释：在生成模型中，我们有两组样本：一组是真实数据的样本(\(S_1\))，另一组是模型生成的样本(\(S_2\))。我们希望这两组样本尽可能相似，这样就意味着我们的模型能够生成与真实数据相似的样本。但在高维空间中（如图像数据，可能有数百万维），直接比较这种相似性变得非常困难。因此，我们转而使用一种间接方法：训练一个模型来区分这两组样本，然后通过让生成模型"欺骗"这个区分器来提高生成样本的质量。

GAN目标函数

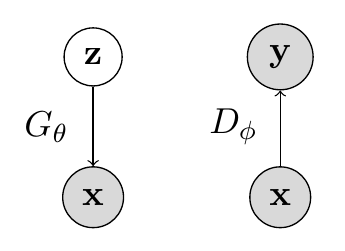
因此，我们得到了生成对抗网络的公式。GAN中有两个组件：(1)生成器和(2)判别器。生成器\(G_\theta\)是一个有向潜变量模型，它确定性地从\(\mathbf{z}\)生成样本\(\mathbf{x}\)，而判别器\(D_\phi\)是一个函数，其工作是区分来自真实数据集和生成器的样本。下图是\(G_\theta\)和\(D_\phi\)的图形模型。\(\mathbf{x}\)表示样本（来自数据或生成器），\(\mathbf{z}\)表示我们的噪声向量，\(\mathbf{y}\)表示判别器对\(\mathbf{x}\)的预测。

解释：

生成器(Generator)：可以想象成一个"造假者"，它试图创造出看起来真实的数据（比如逼真的图像）

判别器(Discriminator)：相当于一个"鉴定专家"，它尝试区分哪些是真实数据，哪些是生成器造出来的"假"数据

\(\mathbf{z}\)：是输入给生成器的随机噪声，可以理解为生成过程的"灵感来源"或"随机种子"

\(\mathbf{x}\)：是数据样本，可能是真实的，也可能是生成的

\(\mathbf{y}\)：是判别器的输出，表示它认为样本是真实的概率

生成器和判别器都在玩一个双人极小极大博弈，其中生成器最小化双样本检验目标(\(p_{\textrm{data}} = p_\theta\))，而判别器最大化目标(\(p_{\textrm{data}} \neq p_\theta\))。直观地说，生成器尽其所能地试图欺骗判别器，生成看起来与\(p_{\textrm{data}}\)无法区分的样本。

解释：这是一个博弈过程，类似于造假者和鉴定专家之间的较量：

造假者(生成器)想要创造出能骗过鉴定专家的假货

鉴定专家(判别器)想要提高自己的鉴别能力，准确识别真假

通过这种不断的"较量"，造假者会越来越擅长创造逼真的假货，这正是我们想要的结果

形式上，GAN目标可以写为：

\[\min_{\theta} \max_{\phi} V(G_\theta, D_\phi) = \mathbb{E}_{\mathbf{x} \sim \textbf{p}_{\textrm{data}}}[\log D_\phi(\textbf{x})] + \mathbb{E}_{\mathbf{z} \sim p(\textbf{z})}[\log (1-D_\phi(G_\theta(\textbf{z})))]\]

解释：这个公式看起来复杂，但可以分解理解：

\(\min_{\theta} \max_{\phi}\)：表示我们要找到参数\(\theta\)使目标函数最小，同时找到参数\(\phi\)使目标函数最大

第一项\(\mathbb{E}_{\mathbf{x} \sim \textbf{p}_{\textrm{data}}}[\log D_\phi(\textbf{x})]\)：是判别器对真实数据的预测结果。\(\mathbb{E}\)表示期望（平均值）。这一项越大，说明判别器越能正确识别真实数据

第二项\(\mathbb{E}_{\mathbf{z} \sim p(\textbf{z})}[\log (1-D_\phi(G_\theta(\textbf{z})))]\)：是判别器对生成数据的预测结果。这一项越大，说明判别器越能正确识别生成的假数据

判别器想要最大化整个表达式（提高鉴别能力），而生成器想要最小化整个表达式（提高造假能力）

让我们解析这个表达式。我们知道判别器相对于其参数\(\phi\)最大化这个函数，其中给定一个固定的生成器\(G_\theta\)，它执行二元分类：它为来自训练集的数据点\(\mathbf{x} \sim p_{\textrm{data}}\)分配概率1，为生成的样本\(\mathbf{x} \sim p_G\)分配概率0。在这种设置下，最优判别器是：

\[D^*_{G}(\mathbf{x}) = \frac{p_{\textrm{data}}(\mathbf{x})}{p_{\textrm{data}}(\mathbf{x}) + p_G(\mathbf{x})}\]

解释：这个公式给出了理论上最优的判别器。它表示在点\(\mathbf{x}\)处，判别器应该输出的最佳概率值。这个概率等于真实数据在该点的概率密度除以真实数据和生成数据在该点的概率密度之和。简单来说，如果在某点真实数据更可能出现，判别器就应该给出更接近1的值；如果生成数据更可能出现，判别器就应该给出更接近0的值。

另一方面，生成器对于固定的判别器\(D_\phi\)最小化这个目标。经过一些代数运算，将最优判别器\(D^*_G(\cdot)\)代入整体目标\(V(G_\theta, D^*_G(\mathbf{x}))\)，得到：

\[2D_{\textrm{JSD}}[p_{\textrm{data}}, p_G] - \log 4\]

\(D_{\textrm{JSD}}\)项是Jensen-Shannon散度，也被称为KL散度的对称形式：

\[D_{\textrm{JSD}}[p, q] = \frac{1}{2} \left( D_{\textrm{KL}}\left[p, \frac{p+q}{2} \right] + D_{\textrm{KL}}\left[q, \frac{p+q}{2} \right] \right)\]

解释：

散度(Divergence)是衡量两个概率分布之间差异的度量

KL散度(Kullback-Leibler divergence)是常用的一种散度，但它不是对称的，即\(D_{KL}[p,q] \neq D_{KL}[q,p]\)

Jensen-Shannon散度是KL散度的一种变体，它是对称的，即\(D_{JSD}[p,q] = D_{JSD}[q,p]\)

这个公式表示，JS散度等于两个分布分别与它们的平均分布之间的KL散度的平均值

在GAN中，我们希望生成的数据分布\(p_G\)与真实数据分布\(p_{\textrm{data}}\)之间的JS散度尽可能小

JSD满足KL的所有性质，并且有额外的优点\(D_{\textrm{JSD}}[p,q] = D_{\textrm{JSD}}[q,p]\)。使用这个距离度量，GAN目标的最优生成器变为\(p_G = p_{\textrm{data}}\)，我们可以用最优生成器和判别器\(G^*(\cdot)\)和\(D^*_{G^*}(\mathbf{x})\)达到的最优目标值是\(-\log 4\)。

GAN训练算法

因此，我们训练GAN的方式如下：

对于轮次1, \(\ldots\), N：

从数据中采样大小为m的小批量：\(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(m)} \sim \mathcal{D}\)
采样大小为m的噪声小批量：\(\mathbf{z}^{(1)}, \ldots, \mathbf{z}^{(m)} \sim p_z\)
对生成器参数\(\theta\)进行梯度下降步骤：
\[\triangledown_\theta V(G_\theta, D_\phi) = \frac{1}{m} \triangledown_\theta \sum_{i=1}^m \log \left(1 - D_\phi(G_\theta(\mathbf{z}^{(i)})) \right)\]
对判别器参数\(\phi\)进行梯度上升步骤：
\[\triangledown_\phi V(G_\theta, D_\phi) = \frac{1}{m} \triangledown_\phi \sum_{i=1}^m \left[\log D_\phi(\mathbf{x}^{(i)}) + \log (1 - D_\phi(G_\theta(\mathbf{z}^{(i)}))) \right]\]

解释：

首先，我们从真实数据中抽取一批样本

然后，我们生成一批随机噪声作为生成器的输入

接着，我们更新生成器的参数，目标是让判别器误以为生成的样本是真实的（注意这里是梯度下降，因为生成器要最小化目标函数）

最后，我们更新判别器的参数，目标是提高它区分真实样本和生成样本的能力（这里是梯度上升，因为判别器要最大化目标函数）

这个过程不断重复，生成器和判别器在这个"博弈"中不断提高各自的能力。

挑战

尽管GANs已成功应用于多个领域和任务，但在实践中使用它们具有挑战性，因为它们：(1)优化过程不稳定，(2)可能出现模式崩溃，(3)评估困难。

解释：

优化过程不稳定：指训练过程中生成器和判别器的损失函数可能会剧烈波动，难以收敛

模式崩溃(mode collapse)：指生成器可能只学会产生有限几种类型的样本，而不是学习整个数据分布。例如，在生成人脸图像时，可能只生成几种特定表情或角度的脸，而不是多样化的人脸

评估困难：指难以客观地评估GAN的性能好坏，因为没有一个统一的标准来衡量生成样本的质量

在优化过程中，生成器和判别器的损失通常会继续振荡，而不会收敛到一个明确的停止点。由于缺乏稳健的停止标准，很难知道GAN何时完成训练。此外，GAN的生成器经常会陷入反复生成几种类型样本的情况（模式崩溃）。对这些挑战的大多数修复方法都是基于经验驱动的，已经有大量工作致力于开发新的架构、正则化方案和噪声扰动，试图规避这些问题。Soumith Chintala有一个不错的链接，概述了各种稳定GAN训练的技巧。

精选GANs

接下来，我们将注意力集中在几种精选的GAN架构上，并更详细地探讨它们。

f-GAN

f-GAN优化了我们迄今讨论的双样本检验目标的变体，但使用了一种非常通用的距离概念：f散度。给定两个密度p和q，f-散度可以写为：

\[D_f(p,q) = \mathbb{E}_{\mathbf{x}\sim q}\left[f \left(\frac{p(\mathbf{x})}{q(\mathbf{x})} \right) \right]\]

其中f是任何凸¹、下半连续²的函数，且f(1) = 0。我们迄今见过的几种距离"度量"都属于f-散度类，如KL、Jensen-Shannon和总变差。

解释：

f-GAN是一种更通用的GAN框架，它允许使用不同类型的散度来衡量真实分布和生成分布之间的差异

f散度是一类散度的总称，通过选择不同的函数f，可以得到不同类型的散度

例如，当f(x)=x log x时，f散度就是KL散度；当f(x)=-log x时，f散度就是反向KL散度

这种灵活性使得f-GAN可以适应不同类型的数据和任务

为了设置f-GAN目标，我们借用凸优化³中常用的两个工具：Fenchel共轭和对偶性。具体来说，我们通过其Fenchel共轭获得任何f-散度的下界：

\[D_f(p,q) \geq \sup_{T \in \mathcal{T}} \left(\mathbb{E}_{x \sim p}[T(\mathbf{x})] - \mathbb{E}_{x \sim q}[f^*(T(\mathbf{x}))] \right)\]

解释：

Fenchel共轭是凸分析中的一个概念，可以用来将一个函数转换为另一个函数

这个公式给出了f散度的一个下界，这个下界可以通过优化函数T来逼近真实的f散度

在实践中，我们可以用神经网络来参数化函数T，然后通过优化这个神经网络来最大化这个下界

因此，我们可以选择任何我们想要的f-散度，令p = \(p_{\textrm{data}}\)和q = \(p_G\)，用\(\phi\)参数化T，用\(\theta\)参数化G，得到以下fGAN目标：

\[\min_\theta \max_\phi F(\theta,\phi) = \mathbb{E}_{x \sim p_{\textrm{data}}}[T_\phi(\mathbf{x})] - \mathbb{E}_{x \sim p_{G_\theta}}[f^*(T_\phi(\mathbf{x}))]\]

直观地说，我们可以将这个目标视为生成器试图最小化散度估计，而判别器试图收紧下界。

BiGAN

在这些笔记中，我们不会太担心BiGAN。然而，我们可以将这个模型视为一个允许我们在GAN框架内推断潜在表示的模型。

解释：

传统的GAN只能从随机噪声生成数据，但不能反向操作（即从数据推断出对应的潜在表示）

BiGAN通过引入一个额外的编码器网络，使得GAN能够双向操作：既可以从噪声生成数据，也可以从数据推断出对应的潜在表示

这使得BiGAN可以用于特征学习和表示学习，而不仅仅是生成样本

CycleGAN

CycleGAN是一种允许我们进行无监督图像到图像转换的GAN，在两个域\(\mathcal{X} \leftrightarrow \mathcal{Y}\)之间。

解释：

无监督图像到图像转换是指在没有成对数据的情况下，学习将一种类型的图像转换为另一种类型

例如，将马的图像转换为斑马的图像，或者将夏季景色转换为冬季景色

传统的图像转换方法需要成对的数据（即同一场景的两种不同风格的图像），而CycleGAN不需要这种成对数据

具体来说，我们学习两个条件生成模型：G: \(\mathcal{X} \leftrightarrow \mathcal{Y}\)和F: \(\mathcal{Y} \leftrightarrow \mathcal{X}\)。有一个与G相关的判别器\(D_\mathcal{Y}\)，比较真实的Y与生成的样本\(\hat{Y} = G(X)\)。类似地，有另一个与F相关的判别器\(D_\mathcal{X}\)，比较真实的X与生成的样本\(\hat{X} = F(Y)\)。下图说明了CycleGAN设置：

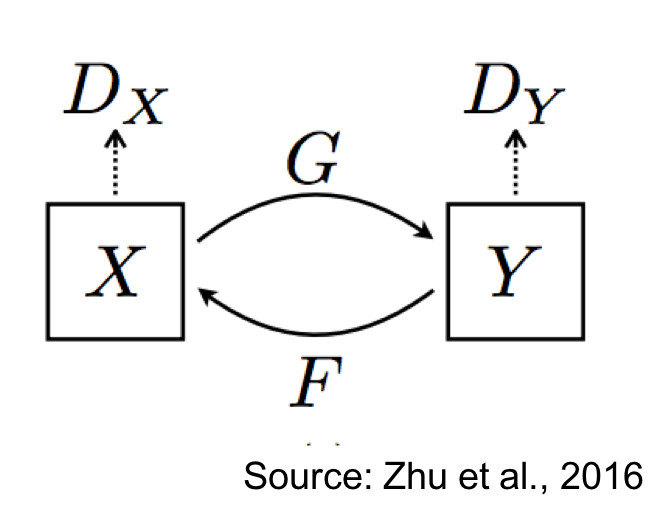
CycleGAN强制执行一种称为循环一致性的属性，该属性指出，如果我们可以通过G从X到\(\hat{Y}\)，那么我们也应该能够通过F从\(\hat{Y}\)到X。整体损失函数可以写为：

\[\min_{F, G, D_\mathcal{X}, D_\mathcal{Y}} \mathcal{L}_{GAN}(G, D_\mathcal{Y}, X, Y) + \mathcal{L}_{GAN}(F, D_\mathcal{X}, X, Y) + \lambda \left(\mathbb{E}_X [||F(G(X)) - X||_1] + \mathbb{E}_Y [||G(F(Y)) - Y||_1] \right)\]

解释：

循环一致性是CycleGAN的核心思想，它要求转换过程是可逆的

第一项是G的GAN损失，确保G生成的Y看起来像真实的Y

第二项是F的GAN损失，确保F生成的X看起来像真实的X

第三项是循环一致性损失，它有两部分：

\(\mathbb{E}_X [||F(G(X)) - X||_1]\)：确保将X转换为Y后再转换回来，得到的结果应该接近原始的X

\(\mathbb{E}_Y [||G(F(Y)) - Y||_1]\)：确保将Y转换为X后再转换回来，得到的结果应该接近原始的Y

\(\lambda\)是一个权重参数，用来平衡GAN损失和循环一致性损失

脚注

¹ 在这种情况下，凸意味着连接任意两点的线位于函数上方。简单来说，如果我们在函数上取两个点，然后画一条连接这两点的直线，那么这条线上的所有点都应该在函数图像的上方或者恰好在函数图像上。这是一种数学上严格定义凸函数的方式。

² 函数在任何点\(\mathbf{x}_0\)的值接近或大于f(\(\mathbf{x}_0\))。下半连续性是一种数学性质，它确保函数在某点的极限不会突然跳到一个更小的值。简单来说，如果我们沿着一条路径接近某个点，函数值不会突然下降。

³ 这本书是学习这些主题的优秀资源。凸优化是数学优化的一个子领域，专注于凸函数的最小化（或等价地，凸函数的最大化）。它在机器学习、统计学、工程学等多个领域有广泛应用。

上一章：标准化流模型