引言

智能体不断地生成、获取和处理数据。这些数据可能是我们在手机上拍摄的图像，与朋友分享的文本消息，模拟社交媒体互动的图表，记录重要事件的视频等。自然智能体擅长发现模式、提取知识并基于观察到的数据进行复杂推理。我们如何构建人工学习系统来做同样的事情？

解释：这里的"智能体"（agent）是指能够感知环境并采取行动的实体，可以是人类、动物或人工系统。在人工智能领域，智能体通常指能够自主决策和学习的计算系统。

在本课程中，我们将研究以概率视角看待世界的生成模型。在这种世界观中，我们可以将任何类型的观察数据（比如 \(\mathcal{D}\)）视为来自底层分布（比如 \(p_{\mathrm{data}}\)）的有限样本集。任何生成模型的核心目标是在获取数据集 \(\mathcal{D}\) 的情况下近似这个数据分布。希望如果我们能够学习一个好的生成模型，我们可以使用学习到的模型进行下游推断。

解释：生成模型（Generative Model）是一类机器学习模型，它们试图学习数据的真实分布，以便能够生成新的、类似于训练数据的样本。这里的 \(\mathcal{D}\) 表示我们收集的数据集，而 \(p_{\mathrm{data}}\) 表示这些数据背后的真实概率分布。例如，如果 \(\mathcal{D}\) 是一组狗的图像，那么 \(p_{\mathrm{data}}\) 就是所有可能的狗图像的分布。生成模型的目标是学习一个近似分布 \(p_\theta\)，使其尽可能接近 \(p_{\mathrm{data}}\)。

学习

我们主要关注数据分布的参数化近似，它将数据集 \(\mathcal{D}\) 的所有信息汇总到有限的参数集中。与非参数模型相比，参数模型在大型数据集上扩展更有效，但在它们能表示的分布族方面受到限制。

解释：参数化模型（Parametric Model）使用固定数量的参数来表示数据分布，这些参数的数量不随训练数据量增加而增加。例如，一个高斯分布可以用均值和方差两个参数完全描述。相比之下，非参数化模型（Non-parametric Model）的参数数量会随着训练数据量的增加而增加。参数化模型的优点是计算效率高、存储需求小，缺点是表达能力可能受限；非参数化模型则相反，表达能力强但计算和存储成本高。在生成模型中，我们通常使用参数化模型，如神经网络，它们有固定数量的权重和偏置参数。

在参数化设置中，我们可以将学习生成模型的任务视为在模型分布族中选择参数，以最小化模型分布与数据分布之间的某种距离¹。

解释：这里的"距离"是指衡量两个概率分布之间差异的度量。在数学上，严格的距离度量（metric）需要满足四个条件：非负性、同一性、对称性和三角不等式。然而，在生成模型中，我们经常使用不满足所有这些条件的"距离"，如KL散度（Kullback-Leibler divergence）。KL散度衡量一个概率分布相对于另一个的信息损失，它不满足对称性（即 \(KL(P||Q) \neq KL(Q||P)\)）和三角不等式。

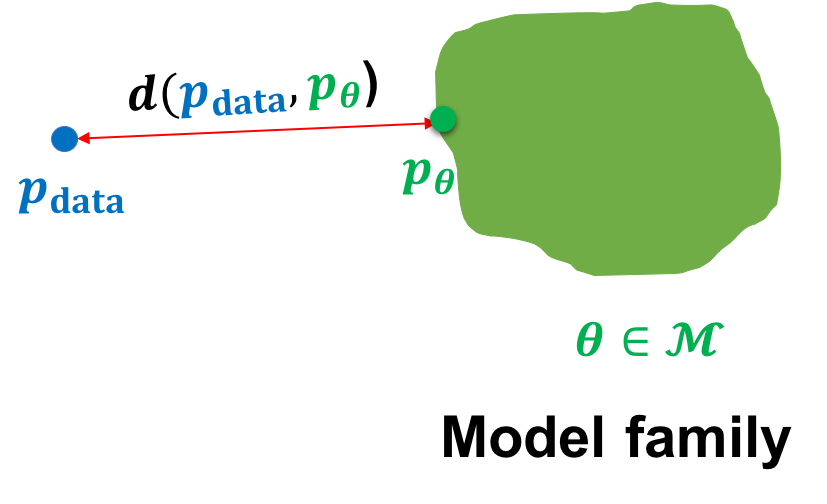
例如，我们可能获得了一个狗图像数据集 \(\mathcal{D}\)，我们的目标是在模型族 \(\mathcal{M}\) 中学习生成模型的参数 \(\theta\)，使得模型分布 \(p_\theta\) 接近狗的数据分布 \(p_{\mathrm{data}}\)。数学上，我们可以将目标指定为以下优化问题：

\[\min_{\theta\in \mathcal{M}}d(p_{\mathrm{data}}, p_{\theta}) \tag{1}\]

其中 \(p_{\mathrm{data}}\) 通过数据集 \(\mathcal{D}\) 访问，\(d(\cdot)\) 是概率分布之间的距离度量。

解释：这个公式表示我们要找到模型参数 \(\theta\)，使得模型分布 \(p_\theta\) 和真实数据分布 \(p_{\mathrm{data}}\) 之间的距离 \(d\) 最小化。模型族 \(\mathcal{M}\) 是所有可能的参数配置的集合。在实践中，我们无法直接访问真实分布 \(p_{\mathrm{data}}\)，只能通过数据集 \(\mathcal{D}\) 间接了解它。常用的距离度量包括KL散度、Wasserstein距离、Jensen-Shannon散度等。不同的距离度量会导致不同的优化目标和学习行为。

在学习本课程的过程中，了解所面临问题的难度是很有意思的。现代手机相机的典型图像分辨率约为 \(700 \times 1400\) 像素。每个像素有三个通道：红(R)、绿(G)和蓝(B)，每个通道的值在0到255之间。因此，可能的图像数量为 \(256^{700 \times 1400 \times 3} \approx 10^{800000}\)。相比之下，ImageNet（一个最大的公开可用数据集之一）仅包含约1500万张图像。因此，用如此有限的数据集学习生成模型是一个高度欠定的问题。

解释：欠定问题（underdetermined problem）是指未知数的数量超过方程数的问题，通常有无穷多个解。在生成模型中，我们试图从有限的样本（如1500万张图像）中学习一个能够表示所有可能图像（\(10^{800000}\)个）的分布，这是一个典型的欠定问题。这个例子说明了生成模型面临的挑战：可能的数据空间极其庞大，而我们只能观察到其中极小的一部分。这就需要模型能够有效地泛化，从有限的观察中捕捉数据的本质特征。

幸运的是，现实世界具有高度结构化的特性，自动发现底层结构是学习生成模型的关键。例如，即使只有几张图像，我们也可以希望学习关于狗的一些基本特征：两只眼睛、两只耳朵、毛发等。我们不会明确地纳入这种先验知识，而是希望模型直接从数据中学习底层结构。然而，没有免费的午餐，成功学习生成模型确实需要以适当的方式实例化公式(1)中的优化问题。在本课程中，我们将主要关注以下问题：

• 模型族 \(\mathcal{M}\) 的表示是什么？
• 目标函数 \(d(\cdot)\) 是什么？
• 最小化 \(d(\cdot)\) 的优化程序是什么？

解释：

1. 模型族 \(\mathcal{M}\) 的表示是指我们如何构建生成模型的结构，例如使用自回归模型、变分自编码器、生成对抗网络等不同架构。
2. 目标函数 \(d(\cdot)\) 是指我们如何衡量模型分布与真实分布的差异，如KL散度、最大似然估计等。
3. 优化程序是指我们如何调整模型参数以最小化目标函数，如梯度下降、Adam优化器等算法。

这三个方面共同决定了生成模型的学习过程和最终性能。

在接下来的几组讲座中，我们将深入研究某些生成模型族。对于每个模型族，我们将注意表示如何与学习目标和优化程序的选择紧密相连。

推断

对于诸如逻辑回归之类的判别模型，基本推断任务是为任何给定数据点预测标签。另一方面，生成模型学习整个数据的联合分布。²

解释：判别模型（Discriminative Model）和生成模型（Generative Model）是机器学习中两种主要的模型类型。判别模型学习条件概率分布 \(P(Y|X)\)，即给定输入 \(X\) 预测输出 \(Y\) 的概率。例如，逻辑回归学习 \(P(类别|特征)\)。而生成模型学习联合概率分布 \(P(X,Y)\) 或数据分布 \(P(X)\)，它不仅能预测输出，还能生成新的数据样本。判别模型通常在分类任务中表现更好，而生成模型则在数据生成、异常检测等任务中更有优势。

虽然生成模型应用的范围不断扩大，但我们可以确定三个基本推断查询来评估生成模型：

1. 密度估计：给定数据点 \(\mathbf{x}\)，模型分配的概率是多少，即 \(p_\theta(\mathbf{x})\)？

   解释：密度估计（Density Estimation）是评估一个数据点在概率分布中的可能性。在生成模型中，我们希望模型能够给真实数据点分配高概率，给不真实或不相关的数据点分配低概率。例如，一个好的狗图像生成模型应该给真实的狗图像分配高概率，给猫图像或随机噪声分配低概率。密度估计可用于异常检测、数据压缩等任务。

2. 采样：我们如何从模型分布中生成新颖数据，即 \(\mathbf{x}_{\mathrm{new}} \sim p_\theta(\mathbf{x})\)？

   解释：采样（Sampling）是从学习到的概率分布中生成新数据的过程。符号 \(\mathbf{x}_{\mathrm{new}} \sim p_\theta(\mathbf{x})\) 表示从分布 \(p_\theta(\mathbf{x})\) 中抽取样本 \(\mathbf{x}_{\mathrm{new}}\)。不同的生成模型有不同的采样方法，如自回归模型的顺序采样、变分自编码器的潜变量采样、生成对抗网络的噪声转换等。采样是生成模型最直观的应用，可用于图像生成、文本生成、音乐创作等。

3. 无监督表示学习：我们如何为数据点 \(\mathbf{x}\) 学习有意义的特征表示？

   解释：无监督表示学习（Unsupervised Representation Learning）是指在没有标签的情况下，学习数据的低维表示或特征。这些表示应该捕捉数据的本质特征和结构。在生成模型中，这通常涉及学习一个编码器，将高维数据映射到低维潜在空间。例如，变分自编码器（VAE）学习一个将图像映射到潜在向量的编码器，这些潜在向量可以捕捉图像的语义特征，如物体类别、姿态、颜色等。好的表示学习可以促进下游任务，如分类、聚类和检索。

回到我们学习狗图像生成模型的例子，我们可以直观地期望一个好的生成模型如下工作。对于密度估计，我们期望 \(p_\theta(\mathbf{x})\) 对狗图像较高，否则较低。暗示生成模型的名称，采样涉及生成超出我们在数据集中观察到的新颖狗图像。最后，表示学习可以帮助发现数据中的高级结构，如狗的品种。

解释：这个例子具体说明了生成模型的三个基本任务在狗图像生成中的应用：

1. 密度估计：模型应该能够区分狗图像和非狗图像，给前者分配高概率，后者分配低概率。
2. 采样：模型应该能够生成新的、逼真的狗图像，这些图像不是简单复制训练数据，而是捕捉了狗的本质特征。
3. 表示学习：模型应该学习到能够区分不同狗品种、姿态、颜色等特征的表示，这些表示可以用于狗品种分类、相似狗图像检索等任务。

鉴于上述推断任务，我们注意到两点警告。首先，生成模型在这些任务上的定量评估本身并不简单（特别是采样和表示学习），是一个活跃的研究领域。存在一些定量指标，但这些指标往往无法反映生成样本和学习表示中理想的定性属性。其次，并非所有模型族都允许在所有这些任务上进行高效和准确的推断。实际上，当前生成模型在推断能力方面的权衡导致了非常多样化的方法发展，正如我们将在本课程中看到的那样。

解释：评估生成模型的性能是一个复杂的问题：

1. 对于密度估计，我们可以使用对数似然或困惑度等指标。
2. 对于采样质量，常用的指标包括Inception Score (IS)、Fréchet Inception Distance (FID)等，但这些指标并不完美，可能无法捕捉人类感知的所有方面。
3. 对于表示学习，评估通常是通过下游任务的性能间接进行的。

不同类型的生成模型在这三个任务上有不同的优势和局限性。例如，自回归模型通常在密度估计上表现出色，但采样可能较慢；GAN在生成高质量样本方面表现优异，但密度估计困难；VAE则在表示学习和密度估计方面有优势，但生成的样本质量可能不如GAN。这种权衡导致了生成模型领域的多样化发展。