变分自编码器 (Variational Autoencoders)

引言

潜变量模型构成了一类丰富的概率模型，能够推断出数据中隐藏的结构。在本文中，我们将研究变分自编码器（VAE），它是一类具有潜变量的强大深度生成模型。

解释：潜变量模型是指包含不可直接观测的隐藏变量的模型。这些隐藏变量通常捕捉数据的底层结构或特征。变分自编码器是一种特殊的深度生成模型，它结合了神经网络的表达能力和变分推断的概率框架，能够学习复杂数据的生成过程。

表示方法

考虑下图所示的有向潜变量模型。

解释：上图展示了VAE的图形模型表示。其中\(z\)表示潜在变量（通常是低维的），\(x\)表示观测变量（如图像）。箭头表示条件依赖关系，即\(x\)依赖于\(z\)。

在上述模型中，\(z\)和\(x\)分别表示潜在变量和观测变量。该模型表示的联合分布为：

\[p_\theta(x, z) = p(x \mid z)p(z)\]

解释：这个等式表示联合概率分布\(p_\theta(x, z)\)可以分解为先验分布\(p(z)\)和条件分布\(p(x \mid z)\)的乘积。\(\theta\)表示模型参数。

从生成建模的角度来看，该模型描述了观测数据\(x\)的生成过程，具体步骤如下：

\begin{align} z &\sim p(z) \\ x &\sim p(x \mid z) \end{align}

解释：这个生成过程包含两个步骤：首先从先验分布\(p(z)\)中采样潜变量\(z\)，然后基于这个潜变量从条件分布\(p(x \mid z)\)中采样观测变量\(x\)。这可以理解为先生成数据的"高级"语义信息，然后基于这些信息生成完整的数据。

如果我们认为潜变量\(z\)以某种方式编码了关于\(x\)的语义信息，那么自然可以将这个生成过程视为首先生成关于\(x\)的"高级"语义信息，然后再完全生成\(x\)。这种观点激发了具有丰富潜变量结构的生成模型，例如层次生成模型\(p(x, z_1, \ldots, z_m) = p(x \mid z_1)\prod_i p(z_i \mid z_{i+1})\)——其中关于\(x\)的信息是分层生成的——以及隐马尔可夫模型等时序模型——其中时间相关的高级信息首先被生成，然后再构建\(x\)。

解释：这段描述了更复杂的潜变量模型结构。层次生成模型中，潜变量本身也有层次结构，信息从高层向低层流动。隐马尔可夫模型则适用于时序数据，其中当前时刻的潜变量依赖于前一时刻的潜变量。这些模型结构能够捕捉更复杂的数据生成过程。

现在考虑一个分布族\(P_z\)，其中\(p(z) \in P_z\)描述了\(z\)上的概率分布。接下来，考虑一个条件分布族\(P_{x\mid z}\)，其中\(p_\theta(x \mid z) \in P_{x\mid z}\)描述了给定\(z\)条件下\(x\)的条件概率分布。那么我们的生成模型假设类是所有可能组合的集合：

\begin{align} P_{x,z} = \{p(x, z) \mid p(z) \in P_z, p(x \mid z) \in P_{x\mid z}\} \end{align}

解释：这里定义了模型的假设空间。\(P_{x,z}\)是所有可能的联合分布的集合，这些分布是由先验分布\(p(z)\)和条件分布\(p(x \mid z)\)组合而成的。在实际应用中，我们会从这个假设空间中选择一个最适合数据的模型。

给定数据集\(D = \{x^{(1)}, \ldots, x^{(n)}\}\)，我们关注以下学习和推断任务：

选择\(p \in P_{x,z}\)使其"最佳"拟合\(D\)。
给定样本\(x\)和模型\(p \in P_{x,z}\)，潜变量\(z\)的后验分布是什么？

解释：这里描述了两个主要任务：(1)学习任务，即找到最能解释观测数据的模型；(2)推断任务，即给定观测数据，推断潜在变量的分布。后者通常称为后验推断，是许多应用的关键步骤，如表示学习、数据压缩等。

学习有向潜变量模型

衡量\(p(x, z)\)与观测数据集\(D\)拟合程度的一种方法是测量数据分布（记为\(p_{\mathrm{data}}(x)\)）与模型边缘分布\(p(x) = \int p(x, z) d z\)之间的Kullback-Leibler（KL）散度。"最佳"拟合数据的分布可以通过最小化KL散度获得：

\begin{align} \min_{p \in P_{x, z}}KL(p_{\mathrm{data}}(x) \| p(x)) \end{align}

解释：KL散度是衡量两个概率分布差异的度量。这里我们希望最小化真实数据分布\(p_{\mathrm{data}}(x)\)与模型边缘分布\(p(x)\)之间的KL散度。直观上，这意味着我们希望模型生成的数据分布尽可能接近真实数据分布。

如前所述，优化KL散度的经验估计等价于最大化数据集\(D\)上的边缘对数似然\(\log p(x)\)：

\begin{align} \max_{p \in P_{x, z}} \sum_{x \in D} \log p(x) = \sum_{x \in D} \log\int p(x, z) d z \end{align}

解释：这个等式表明，最小化KL散度等价于最大化观测数据的对数似然。然而，计算这个对数似然涉及对所有可能的潜变量\(z\)进行积分，这在高维情况下通常是难以处理的。

然而，对于高维\(z\)，这个问题通常是难以处理的，因为它涉及对所有可能的潜在变化源\(z\)进行积分（或在\(z\)离散的情况下求和）。一种选择是通过蒙特卡洛方法估计目标函数。对于任何给定的数据点\(x\)，我们可以获得其边缘对数似然的以下估计：

\[\log p(x) \approx \log \frac{1}{k} \sum_{i=1}^k p(x \vert z^{(i)}) \text{, where } z^{(i)} \sim p(z)\]

解释：这是一种蒙特卡洛估计方法，通过从先验分布\(p(z)\)中采样\(k\)个潜变量样本，然后计算条件概率\(p(x \vert z^{(i)})\)的平均值来近似边缘似然。然而，这种方法在实践中往往会导致梯度估计的高方差。

然而，在实践中，优化上述估计会导致梯度估计的高方差。

与其直接最大化对数似然，另一种方法是构造一个更易于优化的下界。为此，我们注意到评估边缘似然\(p(x)\)至少与评估任何潜向量\(z\)的后验\(p(z \mid x)\)一样困难，因为根据定义\(p(z \mid x) = p(x, z) / p(x)\)。

解释：这里指出了一个重要观察：计算边缘似然\(p(x)\)至少与计算后验分布\(p(z \mid x)\)一样困难。这是因为后验分布的定义中包含了边缘似然作为分母。这个观察促使我们寻找替代方法。

接下来，我们引入一个变分族\(Q\)，其中的分布近似真实但难以处理的后验\(p(z \mid x)\)。此后，我们将假设参数化设置，其中模型族\(P_{x, z}\)中的任何分布都由参数集\(\theta \in \Theta\)指定，变分族\(Q\)中的分布由参数集\(\lambda \in \Lambda\)指定。

解释：变分推断的核心思想是用一个更简单的分布族\(Q\)来近似复杂的后验分布\(p(z \mid x)\)。这个分布族中的每个分布都由参数\(\lambda\)指定。这种方法将难以处理的后验推断问题转化为优化问题：寻找最接近真实后验的变分分布。

给定\(P_{x, z}\)和\(Q\)，我们注意到对于任何\(x\)和所有变分分布\(q_\lambda(z) \in Q\)，以下关系成立：

\begin{align} \log p_\theta(x) &= \log \int p_\theta(x, z) d z \\ &= \log \int \frac{q_\lambda(z)}{q_\lambda(z)} p(x, z) d z\\ &\ge\int q_\lambda(z) \log \frac{p_\theta(x, z)}{q_\lambda(z)} d z \\ &= E_{q_\lambda(z)} \left[\log \frac{p_\theta(x, z)}{q_\lambda(z)}\right] \\ &:=ELBO(x; \theta, \lambda) \end{align}

解释：这个推导得到了一个重要结果：对数似然\(\log p_\theta(x)\)的下界，称为证据下界（Evidence Lower Bound，ELBO）。这个下界是通过引入变分分布\(q_\lambda(z)\)并应用Jensen不等式得到的。ELBO可以被解释为：数据的对数似然减去变分分布与真实后验分布之间的KL散度。

其中我们在最后一步使用了Jensen不等式。证据下界（Evidence Lower Bound，简称ELBO）允许一个可处理的无偏蒙特卡洛估计器：

\begin{align} \frac{1}{k} \sum_{i=1}^k \log \frac{p_\theta(x, z^{(i)})}{q_\lambda(z^{(i)})} \text{, where } z^{(i)} \sim q_\lambda(z) \end{align}

解释：ELBO可以通过从变分分布\(q_\lambda(z)\)中采样\(k\)个样本，然后计算每个样本的对数比率\(\log \frac{p_\theta(x, z^{(i)})}{q_\lambda(z^{(i)})}\)的平均值来估计。这个估计器是无偏的，只要从\(q_\lambda(z)\)中采样和评估其密度是容易的。

我们应该选择哪个变分分布？尽管上述推导对于任何变分参数\(\lambda\)的选择都成立，但下界的紧密程度取决于\(q\)的具体选择。

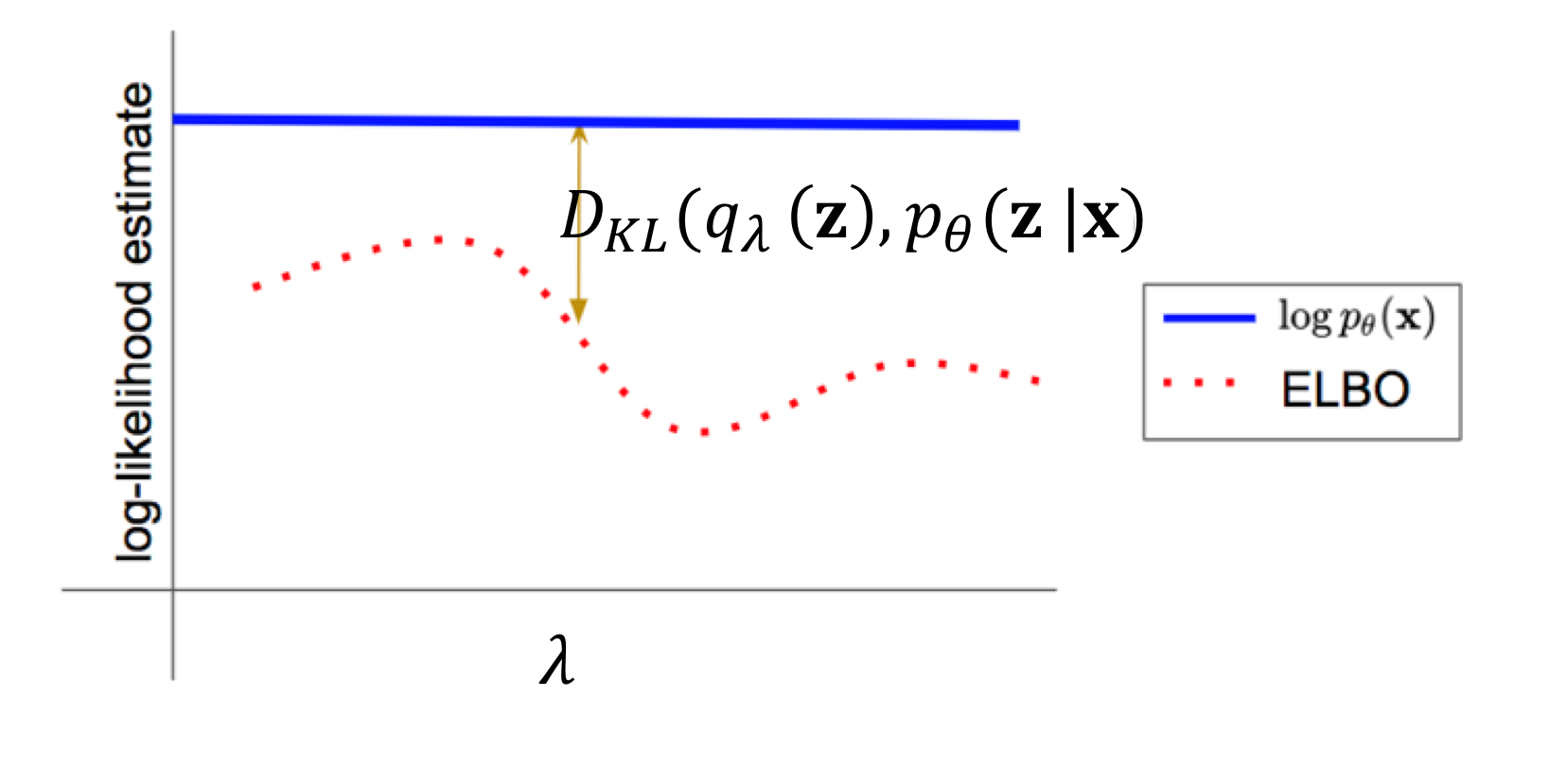
解释：上图说明了数据点\(x\)的边缘对数似然\(\log p_\theta(x)\)与相应ELBO之间的KL散度间隙，这里使用了单个1D参数变分分布\(q_\lambda(x)\)。图中显示了不同\(\lambda\)值对应的ELBO值，以及最优\(\lambda\)值处的ELBO与真实对数似然之间的差距。

特别地，原始目标（边缘对数似然\(\log p_\theta(x)\)）与ELBO之间的差距等于近似后验\(q(z)\)与真实后验\(p(z \mid x)\)之间的KL散度。当变分分布\(q_\lambda(z)\)与\(p_\theta(z \mid x)\)完全匹配时，这个差距为零。

解释：这个观察非常重要：ELBO与真实对数似然之间的差距正好等于变分后验与真实后验之间的KL散度。这意味着，最大化ELBO不仅提高了对数似然的下界，还间接地最小化了变分后验与真实后验之间的差距。

总之，我们可以通过对任何给定数据点\(x\)同时最大化模型参数\(\theta\)和变分参数\(\lambda\)的ELBO来学习潜变量模型：

\begin{align} \max_{\theta} \sum_{x \in D} \max_{\lambda} E_{q_\lambda(z)} \left[\log \frac{p_\theta(x, z)}{q_\lambda(z)}\right] \end{align}

解释：这个优化问题是VAE训练的核心。它包含两个嵌套的最大化：外层对模型参数\(\theta\)的最大化，内层对每个数据点的变分参数\(\lambda\)的最大化。在实践中，这通常通过交替优化\(\theta\)和\(\lambda\)来实现。

黑盒变分推断

在本文中，我们将专注于优化ELBO的一阶随机梯度方法。这些优化技术的优点是允许我们在优化过程中对数据集进行子采样——但要求我们的目标函数对优化变量是可微的。

这启发了黑盒变分推断（Black-Box Variational Inference，BBVI），这是一种用于潜变量模型变分学习的通用期望最大化类算法。对于每个小批量\(M = \{x^{(1)}, \ldots, x^{(m)}\}\)，执行以下两个步骤：

步骤1

首先进行每样本优化\(q\)，通过迭代应用更新：

\begin{align} \lambda^{(i)} \gets \lambda^{(i)} + \tilde{\nabla}_\lambda ELBO(x^{(i)}; \theta, \lambda^{(i)}) \end{align}

解释：在第一步中，我们对每个数据点\(x^{(i)}\)优化其对应的变分参数\(\lambda^{(i)}\)。\(\tilde{\nabla}_\lambda\)表示ELBO梯度的无偏估计。这一步的目的是使变分分布尽可能接近真实后验，从而提高ELBO的紧密度。

其中\(\text{ELBO}(x; \theta, \lambda) = E_{q_\lambda(z)} \left[\log \frac{p_\theta(x, z)}{q_\lambda(z)}\right]\)，\(\tilde{\nabla}_\lambda\)表示ELBO梯度的无偏估计。这一步旨在近似对数似然\(\log p_\theta(x^{(i)})\)。

步骤2

然后基于小批量执行单个更新步骤：

\begin{align} \theta \gets \theta + \tilde{\nabla}_\theta \sum_{i} ELBO(x^{(i)}; \theta, \lambda^{(i)}) \end{align}

解释：在第二步中，我们更新模型参数\(\theta\)。这一步的目的是使模型分布\(p_\theta\)更接近数据分布\(p_{\mathrm{data}}\)。通过最大化所有数据点的ELBO总和，我们间接地最大化了数据的对数似然。

这对应于希望使\(p_\theta\)更接近\(p_{\mathrm{data}}\)的步骤。

梯度估计

梯度\(\nabla_\lambda ELBO\)和\(\nabla_\theta ELBO\)可以通过蒙特卡洛采样估计。虽然构建\(\nabla_\theta ELBO\)的无偏估计很简单，只需将\(\nabla_\theta\)推入期望算子，但对于\(\nabla_\lambda\)则不然。相反，我们看到：

\begin{align} \nabla_\lambda E_{q_\lambda(z)} \left[\log \frac{p_\theta(x, z)}{q_\lambda(z)} \right]= E_{q_\lambda(z)} \left[\left(\log \frac{p_\theta(x, z)}{q_\lambda(z)}\right) \cdot \nabla_\lambda \log q_\lambda(z)\right] \end{align}

解释：这个等式是通过对数导数技巧（也称为REINFORCE技巧）得到的。它允许我们将对期望的梯度转换为期望中的梯度。这个技巧在强化学习和变分推断中都有广泛应用。

这个等式来自对数导数技巧（也常称为REINFORCE技巧）。完整推导涉及一些简单的代数操作，留给读者作为练习。梯度估计器\(\tilde{\nabla}_\lambda ELBO\)因此为：

\begin{align} \frac{1}{k}\sum_{i=1}^k \left[\left(\log \frac{p_\theta(x, z^{(i)})}{q_\lambda(z^{(i)})}\right) \cdot \nabla_\lambda \log q_\lambda(z^{(i)})\right] \text{, where } z^{(i)} \sim q_\lambda(z) \end{align}

解释：这是ELBO关于\(\lambda\)的梯度的蒙特卡洛估计。它通过从\(q_\lambda(z)\)中采样\(k\)个样本，然后计算每个样本的对数比率与对数概率梯度的乘积的平均值来实现。

然而，人们常常注意到这个估计器存在高方差问题。变分自编码器论文的关键贡献之一是重参数化技巧，它引入了一个固定的辅助分布\(p(\varepsilon)\)和一个可微函数\(T(\varepsilon; \lambda)\)，使得以下过程：

\begin{align} \varepsilon &\sim p(\varepsilon)\\ z &\gets T(\varepsilon; \lambda) \end{align}

解释：重参数化技巧是VAE的核心创新之一。它的基本思想是将从\(q_\lambda(z)\)中采样转换为从一个固定分布\(p(\varepsilon)\)中采样，然后通过一个可微函数\(T\)将样本转换为\(z\)。这样做的好处是梯度可以直接通过\(T\)传播，而不需要使用高方差的REINFORCE估计器。

等价于从\(q_\lambda(z)\)中采样。根据无意识统计学家定律，我们可以看到：

\begin{align} \nabla_\lambda E_{q_\lambda(z)} \left[\log \frac{p_\theta(x, z)}{q_\lambda(z)}\right] = E_{p(\varepsilon)} \left[\nabla_\lambda \log \frac{p_\theta(x, T(\varepsilon; \lambda))}{q_\lambda(T(\varepsilon; \lambda))}\right] \end{align}

解释：通过重参数化技巧，我们可以将对\(q_\lambda(z)\)的期望转换为对\(p(\varepsilon)\)的期望。这样，梯度算子可以直接移到期望内部，从而得到一个通常具有更低方差的估计器。

与REINFORCE技巧相比，重参数化技巧经验上被认为具有更低的方差，因此导致更稳定的训练。

通过深度神经网络参数化分布

到目前为止，我们抽象地描述了\(p_\theta(x, z)\)和\(q_\lambda(z)\)。为了实例化这些对象，我们考虑\(p_\theta(z)\)、\(p_\theta(x \mid z)\)和\(q_\lambda(z)\)的参数化分布选择。\(p_\theta(z)\)的一个流行选择是单位高斯分布：

\begin{align} p_\theta(z) = \mathcal{N}(z \mid 0, I) \end{align}

解释：在VAE中，先验分布\(p_\theta(z)\)通常选择为标准正态分布，即均值为零、协方差为单位矩阵的多元高斯分布。这是一个简单的选择，使得从先验中采样变得容易。在这种情况下，\(\theta\)实际上是空集，因为先验是一个固定的分布。

在这种情况下，\(\theta\)只是空集，因为先验是一个固定的分布。另一种实践中常用的替代方案是具有可训练均值和协方差参数的高斯混合分布。

条件分布\(p_\theta(x \mid z)\)是我们引入深度神经网络的地方。我们注意到，条件分布可以通过在目标空间\(x\)中定义一个分布族（由\(\omega \in \Omega\)参数化）（即\(p_\omega(x)\)定义了\(x\)上的无条件分布）和一个映射函数\(g_\theta: Z \to \Omega\)来构建。

解释：这里描述了如何构建条件分布\(p_\theta(x \mid z)\)。基本思想是使用神经网络\(g_\theta\)将潜变量\(z\)映射到一个分布的参数\(\omega\)，然后使用这些参数定义\(x\)的分布。这个神经网络通常被称为"解码器"，因为它将潜在编码\(z\)解码为观测数据的分布。

换句话说，\(g_\theta(\cdot)\)定义了条件分布：

\begin{align} p_\theta(x \mid z) = p_\omega(x) \text{ , where } \omega = g_\theta(z) \end{align}

函数\(g_\theta\)也被称为解码分布，因为它将潜在编码\(z\)映射到观测变量\(x\)分布的参数。在实践中，通常将\(g_\theta\)指定为深度神经网络。

在\(p_\theta(x \mid z)\)是高斯分布的情况下，我们可以将其表示为：

\begin{align} p_\theta(x \mid z) = \mathcal{N}(x \mid \mu_\theta(z), \Sigma_\theta(z)) \end{align}

解释：在实践中，条件分布\(p_\theta(x \mid z)\)通常选择为高斯分布，其均值\(\mu_\theta(z)\)和协方差\(\Sigma_\theta(z)\)由神经网络计算。对于图像数据，这相当于假设每个像素都服从高斯分布，其参数由潜变量决定。

其中\(\mu_\theta(z)\)和\(\Sigma_\theta(z)\)是指定给定\(z\)条件下\(x\)的高斯分布的均值和协方差矩阵的神经网络。

最后，提议分布\(q_\lambda(z)\)的变分族需要谨慎选择，以便重参数化技巧成为可能。位置-尺度族中的许多连续分布都可以重参数化。在实践中，另一个流行的选择是高斯分布：

\begin{align} \lambda &= (\mu, \Sigma) \\ q_\lambda(z) &= \mathcal{N}(z \mid \mu, \Sigma)\\ p(\varepsilon) &= \mathcal{N}(z \mid 0, I) \\ T(\varepsilon; \lambda) &= \mu + \Sigma^{1/2}\varepsilon \end{align}

解释：变分分布\(q_\lambda(z)\)通常选择为高斯分布，其均值\(\mu\)和协方差\(\Sigma\)是变分参数\(\lambda\)。重参数化技巧在这种情况下特别简单：从标准正态分布中采样\(\varepsilon\)，然后通过\(\mu + \Sigma^{1/2}\varepsilon\)转换为从\(q_\lambda(z)\)中的样本。这里\(\Sigma^{1/2}\)是\(\Sigma\)的Cholesky分解。

其中\(\Sigma^{1/2}\)是\(\Sigma\)的Cholesky分解。为简单起见，实践者通常将\(\Sigma\)限制为对角矩阵（这将分布族限制为因子化高斯分布）。

摊销变分推断

黑盒变分推断的一个明显限制是步骤1执行了计算昂贵的优化子程序。回想一下，步骤1的目标是找到：

\begin{align} \lambda^* = \arg \max_{\lambda\in \Lambda} ELBO(x; \theta, \lambda) \end{align}

解释：黑盒变分推断的一个主要缺点是需要为每个数据点\(x\)优化变分参数\(\lambda\)，这在计算上是昂贵的。摊销变分推断（Amortized Variational Inference）通过学习一个从\(x\)到\(\lambda\)的映射来解决这个问题，从而"摊销"了计算成本。

对于给定的\(\theta\)，存在一个从\(x\)到\(\lambda^*\)的明确映射。一个关键的认识是这个映射可以被学习。特别地，可以训练一个编码函数（由\(\phi\)参数化）\(f_\phi: X \to \Lambda\)（其中\(\Lambda\)是\(\lambda\)参数的空间）来优化以下目标：

\begin{align} \max_{\phi } \sum_{x \in D} ELBO(x; \theta, f_\phi(x)) \end{align}

解释：这里的关键思想是，我们可以训练一个神经网络\(f_\phi\)，它直接将输入数据\(x\)映射到最优变分参数\(\lambda^*\)，而不需要为每个数据点单独优化\(\lambda\)。这个网络通常被称为"编码器"，因为它将观测数据编码为潜在空间的分布参数。

值得注意的是，此时\(f_\phi(x)\)可以被解释为定义条件分布\(q_\phi(z \mid x)\)。稍微滥用符号，我们定义：

\begin{align} ELBO(x; \theta, \phi) &= E_{q_\phi(z \mid x)} \left[\log \frac{p_\theta(x, z)}{q_\phi(z \mid x)}\right] \end{align}

这种方法被称为摊销变分推断（Amortized Variational Inference），因为它"摊销"了为每个数据点优化变分参数的计算成本。

变分自编码器

变分自编码器（VAE）是一种结合了摊销变分推断和深度神经网络的生成模型。在VAE中，我们使用两个神经网络：

编码器网络：\(f_\phi(x)\)，将输入数据\(x\)映射到潜变量\(z\)的后验分布参数。
解码器网络：\(g_\theta(z)\)，将潜变量\(z\)映射到观测数据\(x\)的条件分布参数。

VAE的训练目标是最大化ELBO：

\begin{align} \max_{\theta, \phi} \sum_{x \in D} ELBO(x; \theta, \phi) \end{align}

通过应用重参数化技巧，我们可以使用随机梯度下降等标准优化方法来优化这个目标。

ELBO的分解

ELBO可以被分解为两个部分：

\begin{align} ELBO(x; \theta, \phi) &= E_{q_\phi(z \mid x)} \left[\log \frac{p_\theta(x, z)}{q_\phi(z \mid x)}\right] \\ &= E_{q_\phi(z \mid x)} \left[\log p_\theta(x \mid z)\right] - KL(q_\phi(z \mid x) \| p_\theta(z)) \end{align}

解释：ELBO可以分解为两项：第一项是重构项，衡量模型重构数据的能力；第二项是正则化项，鼓励变分后验接近先验分布。这种分解提供了对VAE目标的直观理解：我们希望模型能够重构数据（最大化第一项），同时保持潜变量分布的简单性（最小化第二项）。

第一项是重构项（reconstruction term），它衡量模型重构数据的能力。第二项是正则化项（regularization term），它鼓励变分后验\(q_\phi(z \mid x)\)接近先验分布\(p_\theta(z)\)。

这种分解提供了对VAE目标的直观理解：我们希望模型能够重构数据（最大化第一项），同时保持潜变量分布的简单性（最小化第二项）。

VAE的算法

VAE的训练算法可以概括如下：

从数据集中采样一个小批量\(\{x^{(1)}, \ldots, x^{(m)}\}\)。
对于每个数据点\(x^{(i)}\)：
1. 使用编码器网络\(f_\phi(x^{(i)})\)计算变分后验\(q_\phi(z \mid x^{(i)})\)的参数。
2. 使用重参数化技巧从\(q_\phi(z \mid x^{(i)})\)中采样\(z^{(i)}\)。
3. 使用解码器网络\(g_\theta(z^{(i)})\)计算条件分布\(p_\theta(x^{(i)} \mid z^{(i)})\)的参数。
4. 计算ELBO：\(ELBO(x^{(i)}; \theta, \phi) = \log p_\theta(x^{(i)} \mid z^{(i)}) - KL(q_\phi(z \mid x^{(i)}) \| p_\theta(z))\)。
计算小批量的平均ELBO：\(\frac{1}{m}\sum_{i=1}^m ELBO(x^{(i)}; \theta, \phi)\)。
使用梯度上升更新参数\(\theta\)和\(\phi\)。

VAE的应用

VAE已被成功应用于多种任务，包括：

图像生成：通过从先验分布中采样潜变量，然后使用解码器生成新图像。
图像编辑：通过在潜空间中进行插值或操作，然后解码回图像空间。
异常检测：通过识别具有低似然的数据点。
表示学习：使用编码器学习数据的低维表示，用于下游任务。

VAE的局限性

尽管VAE是一种强大的生成模型，但它也有一些局限性：

模糊生成：VAE生成的图像通常比GAN生成的图像更模糊，这可能是由于使用了高斯似然导致的。
后验崩塌：变分后验可能会忽略潜变量的某些维度，导致所谓的"后验崩塌"问题。
表达能力：简单的高斯先验可能限制了模型捕捉复杂数据分布的能力。

研究人员已经提出了许多改进，如使用更复杂的先验分布、更灵活的变分族和改进的训练目标，以解决这些问题。

结论

变分自编码器是一类强大的生成模型，它结合了变分推断的概率框架和深度神经网络的表达能力。通过引入重参数化技巧和摊销变分推断，VAE能够有效地学习复杂数据的生成过程。

VAE的核心思想——使用神经网络参数化分布和通过变分推断学习潜变量模型——已经影响了许多后续工作，包括规范化流（Normalizing Flows）、变分自回归模型（Variational Autoregressive Models）和变分扩散模型（Variational Diffusion Models）等。

随着研究的不断深入，我们期待看到VAE及其变体在更广泛的应用中发挥作用，并为生成建模领域带来更多创新。

上一章：自回归模型 | 下一章：标准化流模型